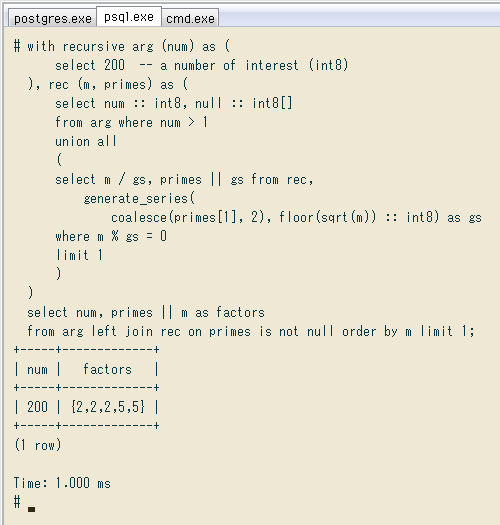
前のブログでも最大公約数とか求めた気がしますが、今回はMATLABのfactor関数と同様の結果をSQLで。PostgreSQL 9.5.3で動作確認してます。
with recursive arg (num) as (
    select 200  -- a number of interest (int8)
), rec (m, primes) as (
    select num :: int8, null :: int8[]
    from arg where num > 1 
    union all
    (
    select m / gs, primes || gs from rec,
        generate_series(
            coalesce(primes[1], 2), floor(sqrt(m)) :: int8) as gs 
    where m % gs = 0
    limit 1
    )
)
select num, primes || m as factors
from arg left join rec on primes is not null order by m limit 1;
+-----+-------------+
| num |   factors   |
+-----+-------------+
| 200 | {2,2,2,5,5} |
+-----+-------------+

↓ ストアド化。上のWITH句の先頭ブロックを引数に変え、他はそのままです。
create or replace function prime_factors(
    in int8, out num int8, out factors int8[])
language sql immutable as 
$$
with recursive arg (num) as (
    select $1
    -- select 200 -- for test
), rec (m, primes) as (
    select num :: int8, null :: int8[]
    from arg where num > 1 
    union all
    (
    select m / gs, primes || gs from rec,
        generate_series(
            coalesce(primes[1], 2), floor(sqrt(m)) :: int8) as gs 
    where m % gs = 0
    limit 1
    )
)
select num, primes || m as factors
from arg left join rec on primes is not null order by m limit 1;
$$;

-- test
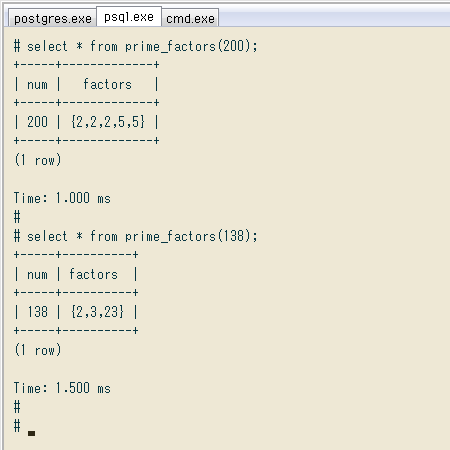
select * from prime_factors(200);
+-----+-------------+
| num |   factors   |
+-----+-------------+
| 200 | {2,2,2,5,5} |
+-----+-------------+

select * from prime_factors(138);
+-----+----------+
| num | factors  |
+-----+----------+
| 138 | {2,3,23} |
+-----+----------+


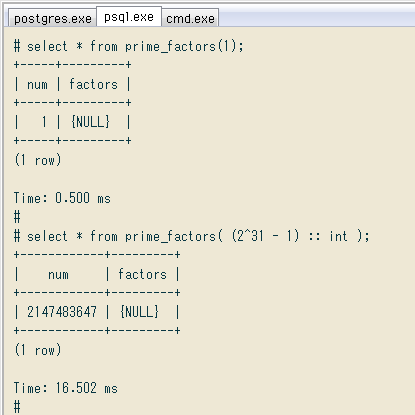
引数が1以下または素因数が見つからない場合（素数）、factorsにNULLを明示します。このためにクエリの最後（WITH句を抜けた後）がちょっと面倒になりました。
select * from prime_factors(1);
+-----+---------+
| num | factors |
+-----+---------+
|   1 | {NULL}  |
+-----+---------+

select * from prime_factors( (2^31 - 1) :: int );
+------------+---------+
|    num     | factors |
+------------+---------+
| 2147483647 | {NULL}  |
+------------+---------+

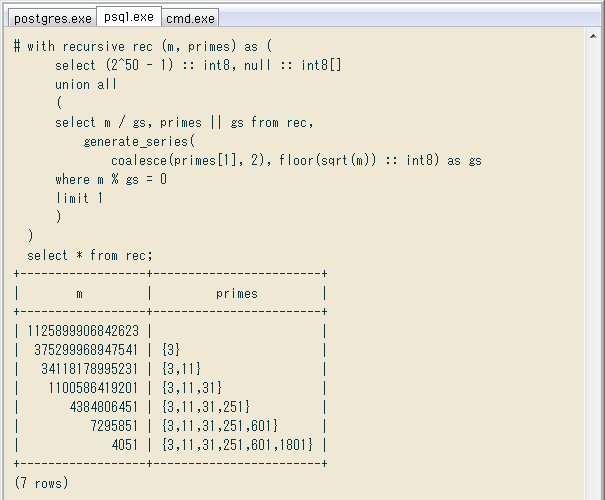
上のとおり32ビット整数（符号あり）の最大値2147483647は素数です。素数判定のページでも確認しました。


動作の流れを明示すると ↓ こんな感じで、「最小の約数を探し、見つかったらそれで割る」ことの再帰です。約数の探索は単純に1ずつ足して割るので無駄が多い…。例えば2で割れなかったら偶数は対象から外すとか（エラトステネスのふるいと同じ）、考えつつまだ上手く実装できていません。
with recursive rec (m, primes) as (
    select (2^50 - 1) :: int8, null :: int8[]
    union all
    (
    select m / gs, primes || gs from rec,
        generate_series(
            coalesce(primes[1], 2), floor(sqrt(m)) :: int8) as gs 
    where m % gs = 0
    limit 1
    )
)
select * from rec;
+------------------+------------------------+
|        m         |         primes         |
+------------------+------------------------+
| 1125899906842623 |                        |
|  375299968947541 | {3}                    |
|   34118178995231 | {3,11}                 |
|    1100586419201 | {3,11,31}              |
|       4384806451 | {3,11,31,251}          |
|          7295851 | {3,11,31,251,601}      |
|             4051 | {3,11,31,251,601,1801} |
+------------------+------------------------+
(7 rows)


このように無駄があるのと、そもそもSQLなので遅いです。Core i5-3320M（2.6GHz）で上と同じ2^50 - 1を調べると ↓ 約7秒。素数だともっとかかります。32ビット整数の範囲ならミリ秒単位ですが。（Windows版PostgreSQL 9.5.3で実行）
# \timing on
# select * from prime_factors( (2^50 - 1) :: int8 ); 
+------------------+-----------------------------+
|       num        |           factors           |
+------------------+-----------------------------+
| 1125899906842623 | {3,11,31,251,601,1801,4051} |
+------------------+-----------------------------+
(1 row)
Time: 6948.882 ms

# select * from prime_factors( (2^31 - 1) :: int );
+------------+---------+
|    num     | factors |
+------------+---------+
| 2147483647 | {NULL}  |
+------------+---------+
(1 row)
Time: 14.002 ms

# select * from prime_factors( (2^31 - 2) :: int );
+------------+-------------------------+
|    num     |         factors         |
+------------+-------------------------+
| 2147483646 | {2,3,3,7,11,31,151,331} |
+------------+-------------------------+
(1 row)
Time: 12.002 ms

速度だけ考えたら再帰クエリでやる意味はなく、自分としてはPostgreSQLで可能なSQLや関数の使い方を知る一環。でも後々、意外な所で役立ったりします。最小の約数を見つける部分を効率的にできたら、追記予定。